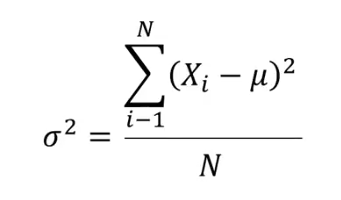این چهارمین بخش از خلاصهی مجموعهی «دورهی مقدماتی data science» هستش.
بخش سوم - تصویرسازی از دادهها و تحلیل آنها
تحلیل آماری
تجزیه و تحلیل آماری رو میشه هستهی اصلی data science دونست. با استفاده از آمار میشه به چگونگی توزیع دادهها، تاثیر اونها بر هم و موارد بسیار زیاد دیگهای پیبرد. نقطهی شروع برای استفاده از آمار در تجزیه و تحلیل دادهها، درک «آمار توصیفی» هستش که با استفاده از اون میتونیم توزیع دادههامون رو تحلیل کنیم.
اگه به ستون دما در جدول اطلاعات فروش لیموناد که در بخشهای قبلی ازش استفاده کردیم توجه کنیم، به چه نتایجی از بازهی دماها میرسیم؟
کمترین مقدار 20.0 هستش که در «نرمافزار اکسل» با تابع ()MIN=، بیشترین مقدار 64.2 هستش که در اکسل با تابع ()MAX= و متوسط دما که با جمع مقادیر و تقسیم اون بر تعداد به دست میاد برابر 44.62 هستش و در اکسل با استفاده از تابع ()AVERAGE= میشه بهش رسید. همونطور که مشخصه مقدار متوسط به احتمال زیاد اصلا بین دادههای موجود وجود نداره.
یه روش دیگه در تحلیل دادهها محاسبهی «میانه» هستش. برای این کار دادهها رو از کوچک به بزرگ مرتب میکنیم و دادهی وسط رو انتخاب کنیم، که اگه این رو روی دماهای ذکر شده در بالا اجرا کنیم، به 46.2 میرسیم. اگر هم تعداد دادهها زوج باشه، از میانگین دو دادهی وسط استفاده میکنیم. در اکسل برای رسیدن به این مقدار از تابع ()MEDIAN= استفاده میشه.
گاهی ممکنه نیاز داشته باشیم بدونیم که در یه بازهی زمانی چه دادهای بیشتر از بقیه تکرار شده که بهش «مُد» گفته میشه. در اعداد تصویر بالا عدد 46.2 دوبار ذکر شده در حالیکه بقیه اعداد یک بار اومدن. در اکسل از تابع ()MODE= برای رسیدن به این مفهوم استفاده میشه. گاهی ممکنه چند عدد مُد باشن، یعنی چند تا عدد داشته باشیم که مثلا دوبار در فهرست دادهها اومده باشن.
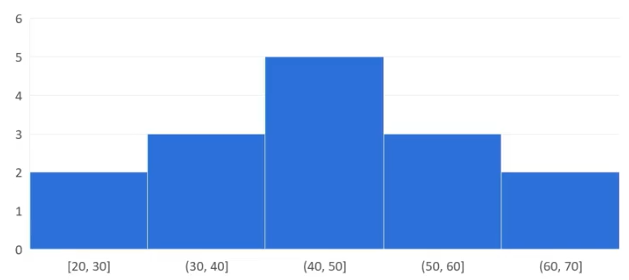
برای تصویرسازی از فراوانی دادهها میشه از نمودار «هیستوگرام» استفاده کرد. در این نمودار، دادهها در دستههایی با بازهی مشخص در محور افقی و تعداد اعضای هر دسته در محور عمودی نمایش داده میشه. نمودار هیستوگرام اعداد بالا به صورت زیر هستش و همونطور که مشخصه، اعداد در بازههایی به طول ۱۰ در محور افقی قرار گرفتن. در این نمودار خیلی سریع میتونیم متوجه شیم که بیشترِ روزها (۵ روز) دمایی در بازهی ۴۰ تا ۵۰ داشتن.
ما معمولا برای اینکه یه دید کلی از دادهها داشته باشیم، به خصوص وقتی حجم دادهها زیاده، از محاسبهی میانگین استفاده میکنیم. اما گاهی ممکنه میانگین ما رو به اشتباه بندازه. به عنوان مثال، اگه دو مجموعه داده داشته باشیم، یکی شامل ۱ و ۹ و دیگری شامل ۶ و ۴، میانگین هر دو مجموعه میشه ۵. اگه در یه گزارش فقط عدد میانگینها رو بگیم، ممکنه این برداشت بوجود بیاد که اعداد دو مجموعه به هم نزدیکن. در حالیکه میبینیم در مجموعهی اول ۸ واحد و در مجموعهی دوم ۲ واحد اختلاف بین اعداد وجود داره، یعنی پراکندگی دادهها تو مجموعهی اول بیشتره. برای حل این مساله از مفهوم «انحراف معیار» و برای محاسبهی انحراف معیار از مفهوم «واریانس» استفاده میکنیم. فرمول ریاضی واریانس به صورت زیر هستش:
ممکنه در ظاهر پیچیده به نظر بیاد ولی ساده است. μ میانگین دادهها و N تعداد دادهها است.Xi هم عضو iاُم مجموعه. در واقع معنیش میشه اینکه اول میانگین دادهها محاسبه و بعد اختلافش با هرکدوم از دادهها به توان ۲ میرسه. بعد مجموع اونها تقسیم بر تعداد دادهها میشه.
برای مجموعهی اول و دوم در مثال بالا، میانگین دادهها برابر با ۵ هستش. برای مجموعهی اول:
۳۲ = ۲(۹-۵) + ۲(۱-۵)
حالا تقسیم ۳۲ بر تعداد اعداد یعنی ۲، واریانس رو به ما میده: ۱۶. اما برای مجموعهی دوم:
۲ = ۲(۶-۵) + ۲(۴-۵)
و اگه ۲ رو تقسیم بر تعداد اعداد یعنی ۲ کنیم واریانس میشه ۱. اون چیزی که ما دنبالش بودیم انحراف معیار بود که در واقع با محاسبهی «جذر» یا ریشهی دوم واریانس به دست میاد. جذر یا ریشهی دوم ۱۶ میشه ۴ و جذر یا ریشهی دوم ۱ هم همون ۱ هستش. این اعداد به علت سادگی مجموعهی دادهی ما، با چشم هم قابل ملاحظه است. یعنی فاصلهی ۱ و ۹ با عدد ۵ (میانگین) برابر ۴ و فاصلهی ۴ و ۶ با عدد ۵ برابر ۱ هستش. همونطور که واضحه، هر چقدر که پراکندگی دادهها کمتر باشه انحراف معیار هم کمتر خواهد بود. در اکسل، برای محاسبهی واریانس از تابع ()VAR.P= و برای محاسبهی انحراف معیار از تابع ()STDEV.P= استفاده میشه.
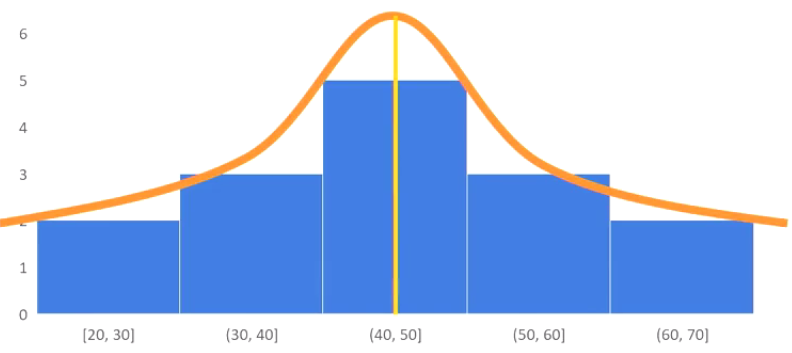
نمودار هیستوگرام نشون میده که نمونه دادههای مربوط به دما که دیدیم، از «توزیع نرمال» پیروی میکنه. در یه توزیع نرمال، میانگین، میانه، مُد و خط تقارن در وسط قرار دارند:
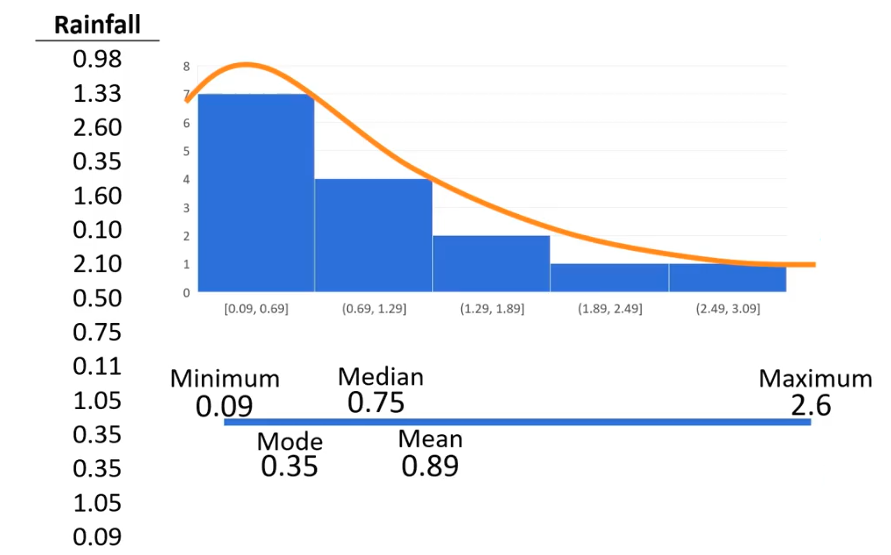
طبیعتا همهی دادهها از توزیع نرمال پیروی نمیکنن. به عنوان مثال، در تصویر زیر دادههای مربوط به مقدار بارندگی، نمودار هیستوگرام و مقادیر میانگین و میانه و مُد مربوطه رو میبینیم. مفهومی که بوسیله نمودار زیر میتونیم بهش بپردازیم تقارن تابع توزیع یا «چولگی» (skewness) هستش. این نمودار دارای چولگی به راست (right skewed) هستش.
رابطه بین فیلدهای مختلف دادهها
گاهی نیاز داریم که رابطهی بین چند فیلد از یه مجموعهی داده رو بدونیم. مثلا میخوایم بدونیم چه رابطهای بین دمای هوا و میزان فروش لیموناد برقراره. قبلا هم دیدیم که برای این کار از نمودار نقشه استفاده میکنیم و روند حاکم بر فیلدها رو بدست میاریم. این همون مفهوم «همبستگی» (correlation) هستش و میشه به صورت عددی میزان این همبستگی رو محاسبه کرد. برای این کار تو اکسل از تابع (,)CORREL= استفاده میشه.
همبستگی دو متغیر، مقداری بین -۱ تا +۱ داره. هر چقدر مقدار همبستگی به ۱ نزدیکتر باشه (+۱ یا -۱)، نشاندهندهی قویتر بودن رابطهی خطی بین دو متغیر هستش. رابطهی خطی یعنی تغییر یکی از متغیرها، مقدار متغیر دیگر را هم تغییر میدهد که این تغییرها میتوانند در یک جهت یا در خلاف جهت باشند. در این صورت میشه روی نمودار نقشه، خطی فرضی با شیب مثبت یا منفی (بر اساس منفی یا مثبت بودن همبستگی) بین نقاط رسم کرد. اما هر چقدر مقدار همبستگی به صفر نزدیکتر باشه، نشاندهندهی پراکندگی دادهها و عدم ارتباط بین تغییرات اونهاست.
در تصویر بالا، بعد از محاسبه میبینیم که میزان همبستگی بین دما و تعداد فروش برابر با 0.93 هستش که خیلی به +۱ نزدیکه و روی نمودار هم میبینیم که خطی با شیب مثبت تونستیم بین نقاط رسم کنیم.
نکتهی آخر در این مورد اینکه، همبستگیِ زیاد بین دو فیلد لزوما به این معنی نیست که تغییر یک فیلد داده، «دلیلِ» تغییر در فیلد دیگه است. بلکه ممکنه فیلد سومی روی هر دو اثر گذاشته باشه یا حتی به طور تصادفی این همبستگی بینشون دیده بشه.
بخش پنجم - مقدمهای بر یادگیری ماشین